Classification

lec10c

Author

Robin Donatello / MATH 615

Published

November 12, 2025

Setup

Code

library(ggplot2)
library(ROCR)
library(ggpubr)
library(caret)
library(gtsummary)
source(here::here("load_data.R"))

Predicted Probabilities

Sometimes Odds Ratios can be difficult to interpret or understand.
Sometimes you just want to report the probability of the event occurring.
Or sometimes you want to predict whether or not a new individual is going to have the event.

For all of these, we need to calculate $p_{i} = P (y_{i} = 1)$ , the probability of the event.

$p_{i} = \frac{e^{β_{0} + β_{1} x_{1 i} + β_{2} x_{2 i} + \dots + β_{p} x_{p i}}}{1 + e^{β_{0} + β_{1} x_{1 i} + β_{2} x_{2 i} + \dots + β_{p} x_{p i}}}$

Example:

Characteristic	log(OR)	95% CI	p-value
age	-0.02	-0.04, 0.00	0.020
income	-0.04	-0.07, -0.01	0.009
sex
Male	—	—
Female	0.93	0.21, 1.7	0.016
Abbreviations: CI = Confidence Interval, OR = Odds Ratio

The predicted probability of depression is calculated as: $P (d e p r e s s e d) = \frac{e^{- 0.676 - 0.02096 * a g e - .03656 * i n c o m e + 0.92945 * s e x}}{1 + e^{- 0.676 - 0.02096 * a g e - .03656 * i n c o m e + 0.92945 * s e x}}$

Notice this formulation requires you to specify a covariate profile. In other words, what value X take on for each record. Often when you are only concerned with comparing the effect of a single measures, you set all other measures equal to their means.

Comparing probabilities

Let’s compare the probability of being depressed for males and females separately, while holding age and income constant at the average value calculated across all individuals (regardless of sex).

$P (d e p r e s s e d | F e m a l e) = \frac{e^{- 0.676 - 0.02096 (44.4) - .03656 (20.6) + 0.92945 (1)}}{1 + e^{- 0.676 - 0.02096 (44.4) - .03656 (20.6) + 0.92945 (1)}} = 0.193$

$P (d e p r e s s e d | M a l e) = \frac{e^{- 0.676 - 0.02096 (44.4) - .03656 (20.6) + 0.92945 (0)}}{1 + e^{- 0.676 - 0.02096 (44.4) - .03656 (20.6) + 0.92945 (0)}} = 0.086$

The probability for a 44.4 year old female who makes $20.6k annual income has a 0.19 probability of being depressed. The probability of depression for a male of equal age and income is 0.086.

Distribution of Predicted probabilities

We can use the predict() command to generate a vector of predictions ${\hat{p}}_{i}$ for each row used in the model.

phat.depr <- predict(dep_sex_model, type='response') 
gghistogram(phat.depr, add = "mean" , fill = "skyblue")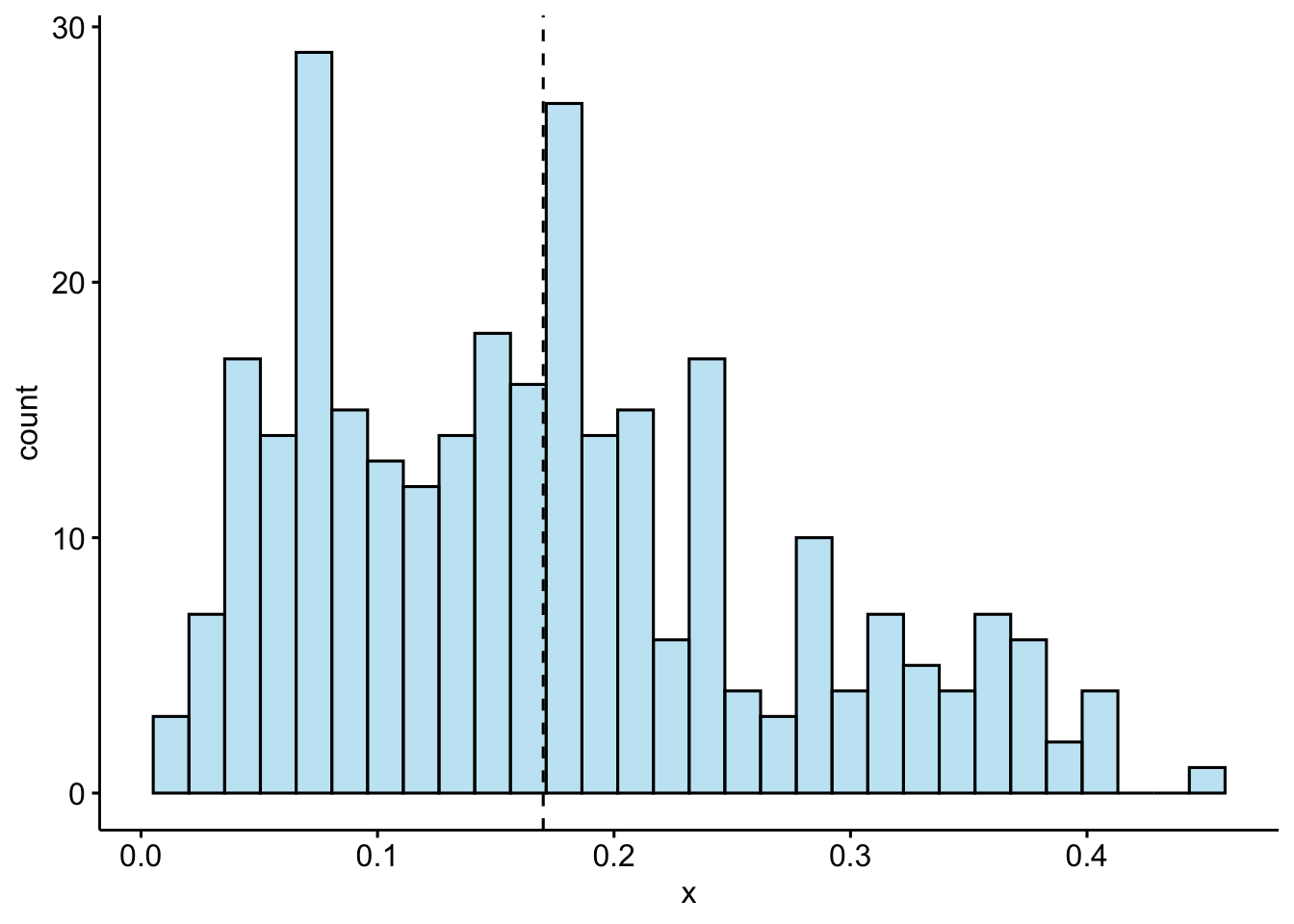

The average predicted probability of showing symptoms of depression is 0.17.

Plotting predictions

There was a significant effect of gender on depression diagnosis. How does that appear in the predicted probabilities?

Handling missing data in the model

Any row with missing data on any variable used in the model will be dropped, and so NOT get a predicted value. So the tactic is to use the data stored in the model object.

Code

model.pred.data <- cbind(dep_sex_model$data, phat.depr)
tail(names(model.pred.data))

[1] "regdoc"    "treat"     "beddays"   "acuteill"  "chronill"  "phat.depr"

Model predicted probability of depression

ggpubr::ggdensity(model.pred.data, x="phat.depr", add="mean", color = "sex", fill = "sex", palette = c("#00AFBB", "#E7B800"))

Reminder this is the fitted data $\hat{p}$
What do you notice in this plot?

Predicted Class (outcome)

To classify individual $i$ as being depressed or not, we draw a binary value ( $x_{i} = 0$ or $1$ ), with probability $p_{i}$ by using the rbinom function, with a size=1.

set.seed(12345) #reminder: change the combo on my luggage
plot.mpp <- data.frame(pred.prob = phat.depr, 
                       pred.class = rbinom(n = length(phat.depr), 
                                           size = 1, 
                                           p = phat.depr),
                       truth = dep_sex_model$y)
head(plot.mpp)

   pred.prob pred.class truth
1 0.21108906          0     0
2 0.08014012          0     0
3 0.15266203          0     0
4 0.24527840          1     0
5 0.15208679          0     0
6 0.17056409          0     0

Confusion Matrix

Applying class labels and creating a cross table of predicted (rows) vs truth (cols):

plot.mpp <- plot.mpp %>% 
            mutate(pred.class = factor(pred.class, labels=c("Not Depressed", "Depressed")), 
                    truth = factor(truth, labels=c("Not Depressed", "Depressed")))

table(plot.mpp$pred.class, plot.mpp$truth)

               
                Not Depressed Depressed
  Not Depressed           195        35
  Depressed                49        15

The model correctly identified 195 individuals as not depressed and 15 as depressed. The model got it wrong 49 + 35 times.

Accuracy

The accuracy of the model is calculated as the fraction of times the model prediction matches the observed category:

(195+15)/(195+35+49+15)

[1] 0.7142857

This model has a 71.4% accuracy.

Is this good?
What if death were the event?

We will see later how to use accuracy as a measure of model fit and how to optimize accuracy by changing the cutoff value.