Inference between two means

Robin Donatello

2024-10-14

Quantitative Outcome ~ Binary Covariate

  • Does knowing what group an observation is in tell you about the location of the data?
  • Are the means of two groups are statistically different from each other?

Model

\[ y_{ij} = \mu_{j} + \epsilon_{ij} \qquad \qquad \epsilon_{ij} \overset{iid}{\sim} \mathcal{N}(0,\sigma^{2}) \]

  • Response data \(y_{ij}\) from observation \(i=1\ldots n\) belonging to group \(j=1,2\)
  • The random error terms \(\epsilon_{ij}\) are independently and identically distributed (iid) as normal with mean zero and common variance.

2 sample T-test for difference in means between two independent groups

  • Parameter: \(\mu_{1} - \mu_{2}\)
  • Estimate: \(\bar{x}_{1} - \bar{x}_{2}\)
  • Assumptions:
    • Group 1 & 2 are mutually exclusive and independent
    • Difference \(\bar{x}_{1} - \bar{x}_{2}\) is normally distributed
    • Variance within each group are approximately the same (\(\sigma\))

\(H_{0}: \mu_{1} - \mu_{2} = 0\): There is no difference in the averages between groups.

\(H_{A}: \mu_{1} - \mu_{2} \neq 0\): There is a difference in the averages between groups.

Example: BMI vs smoking

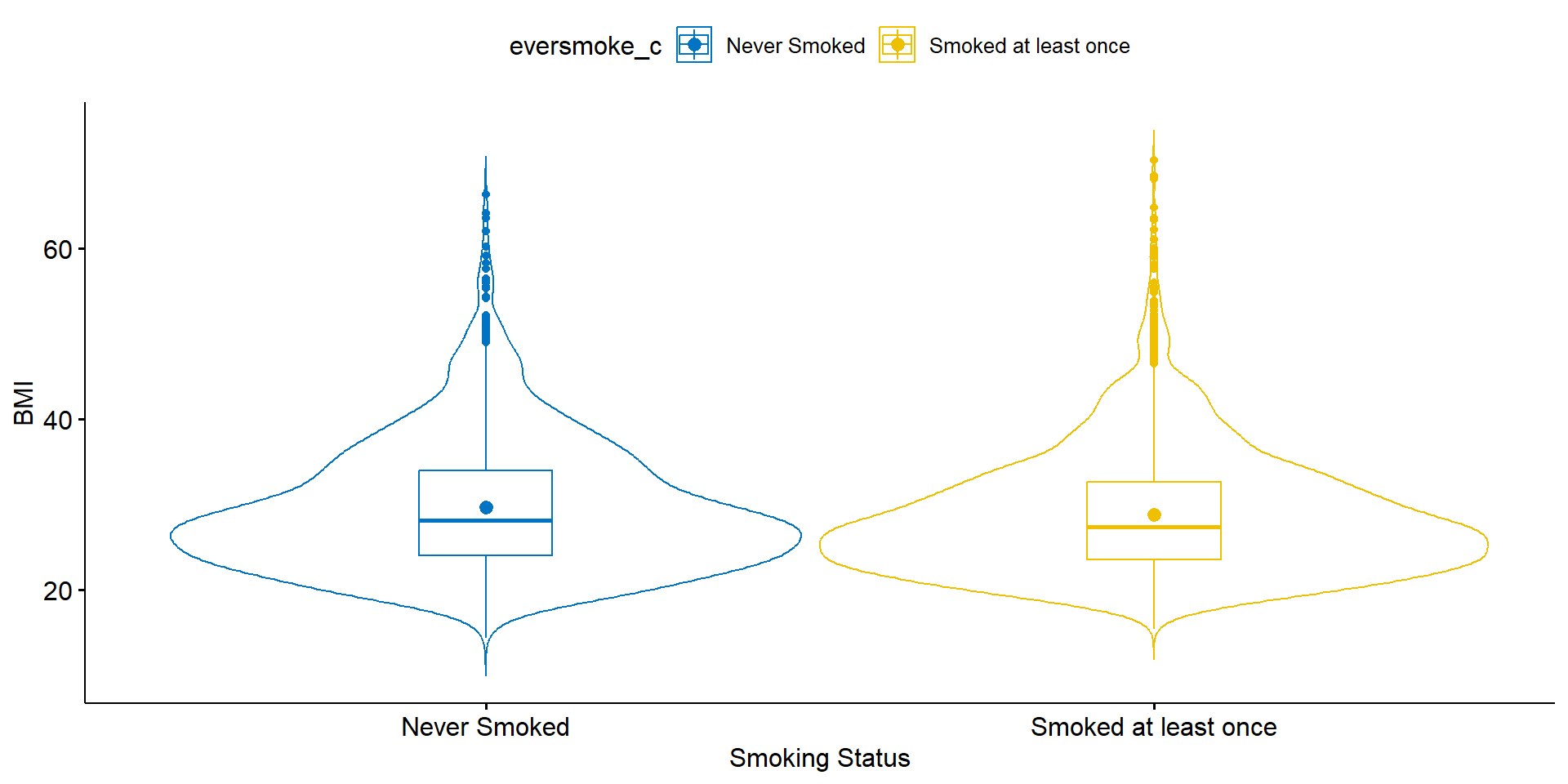
We would like to know, is there convincing evidence that the average BMI differs between those who have ever smoked a cigarette in their life compared to those who have never smoked?

Nitty gritty detail

For the purposes of learning, you will be writing out each step in the analysis in depth. As you begin to master these analyses, it is natural to slowly start to blend and some steps. However it is important for you to have a baseline reference.

1. Identify response and explanatory variables

  • Ever smoker = binary explanatory variable (variable eversmoke_c)
  • BMI = quantitative response variable (variable BMI)

2. Visualize and summarise

Show the code 
plot.bmi.smoke <- addhealth %>% select(eversmoke_c, BMI) %>% na.omit()

plot.bmi.smoke %>% 
  ggviolin(x="eversmoke_c",
    y="BMI",
    color="eversmoke_c", 
    add = c("mean", "boxplot")) + 
  color_palette(palette = "jco") + xlab("Smoking Status")

Show the code 
plot.bmi.smoke %>% 
  tbl_summary(
    by="eversmoke_c",
    digits = all_continuous() ~ 1,     
    statistic = list(
      all_continuous() ~ "{mean} ({sd})"
    ))
Characteristic Never Smoked, N = 1,7501 Smoked at least once, N = 3,2761
BMI 29.7 (7.8) 28.8 (7.3)
1 Mean (SD)

Smokers have on average BMI of 28.8, smaller than the average BMI of non-smokers at 29.7. Non-smokers have more variation in their weights (7.8 vs 7.3lbs), but the distributions both look normal, if slightly skewed right.

3. Write the null and research hypothesis in words and symbols.

Let \(\mu_{1}\) be the average BMI for smokers, and \(\mu_{2}\) be the average BMI for non-smokers


\(H_{0}: \mu_{1} - \mu_{2} = 0\) There is no difference in the average BMI between smokers and non-smokers.


\(H_{A}: \mu_{1} - \mu_{2} \neq 0\) There is a difference in the average BMI between smokers and non-smokers.

4. State and justify the analysis model. Check assumptions.

  • We are comparing the means between two independent samples. A Two-Sample T-Test for a difference in means will be conducted.
  • The assumptions that the groups are independent is upheld because each individual can only be either a smoker or non smoker.
  • The difference in sample means \(\bar{x}_{1}-\bar{x}_{2}\) is normally distributed - this is a valid assumption due to the large sample size and that differences typically are normally distributed.
  • The observations are independent, this was a random sample
  • The variances are roughly equal (67/44 = 1.5 is smaller than 2).

5. Conduct the test and make a decision about the plausibility of the alternative hypothesis.

Show the code 
t.test(BMI ~ eversmoke_c, data=addhealth)

    Welch Two Sample t-test

data:  BMI by eversmoke_c
t = 3.6937, df = 3395.3, p-value = 0.0002245
alternative hypothesis: true difference in means between group Never Smoked and group Smoked at least once is not equal to 0
95 percent confidence interval:
 0.3906204 1.2744780
sample estimates:
        mean in group Never Smoked mean in group Smoked at least once 
                          29.67977                           28.84722

There is strong evidence in favor of the alternative hypothesis. The interval for the differences (0.4, 1.3) does not contain zero and the p-value = .0002.

6. Write a conclusion in context of the problem. Include the point estimates, confidence interval for the difference and p-value.

On average, non-smokers have a significantly higher 0.82 (0.39, 1.27) BMI compared to smokers (p=.0002).

Assumptions

Samples come from the same population

Credit: Allison Horst https://allisonhorst.com/

But we could be wrong

Credit: Allison Horst https://allisonhorst.com/

But we could be wrong

Credit: Allison Horst https://allisonhorst.com/

Type I and Type II Error

  • AKA False positive or false negative. Wikipedia
  • The significance level, \(\alpha\), is what we use to define the amount of “risk” we are willing to take to falsely reject \(H_{0}\) (false positive).
  • We talk more about false positive & false negative, specificity and sensitivity in Math 456.
  • We will see shortly however how to conduct multiple comparisons while maintaining our “family-wise” error rate at \(\alpha\)

🔗 https://math615.netlify.app / Inference between two means