Multiple Linear Regression

Robin Donatello

2024-11-04

Motivation: Life is rarely bivariate.

  • We know that the number of steps someone takes per day is not the only thing that is related to someone’s BMI.
    • diet, age, sex, climate they live in, etc.
  • So how can we understand whether or not physical activity is associated with BMI after controlling for these other measures?
  • Consider two people of the same age, living in the same climate, with the same diet, but their level of physical activity is different.
    • Then we can estimate how much physical activity affects someone’s BMI

Need to expand our model

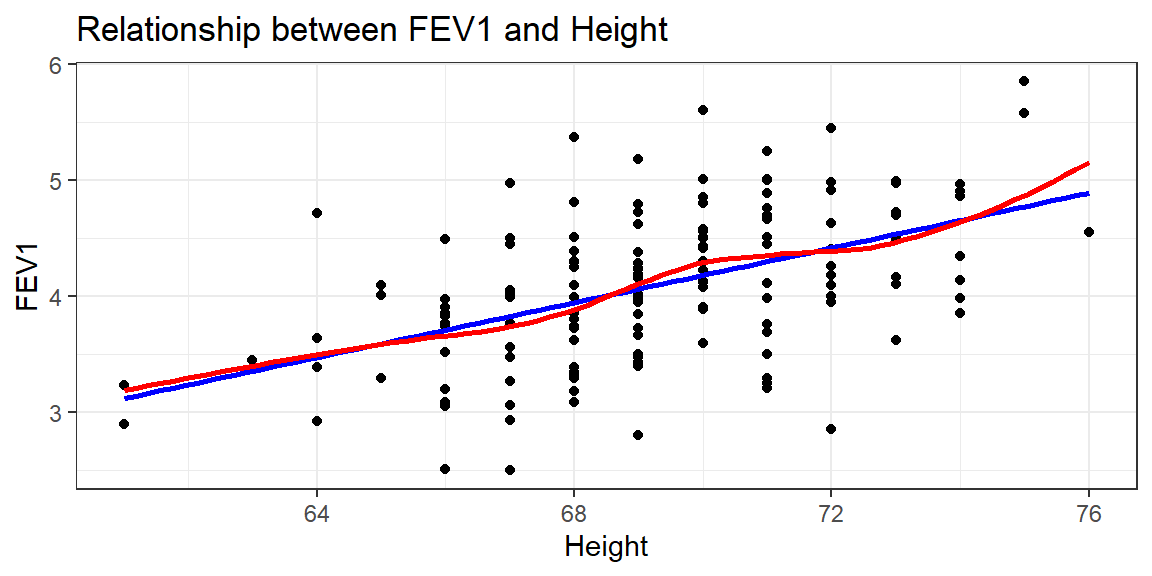
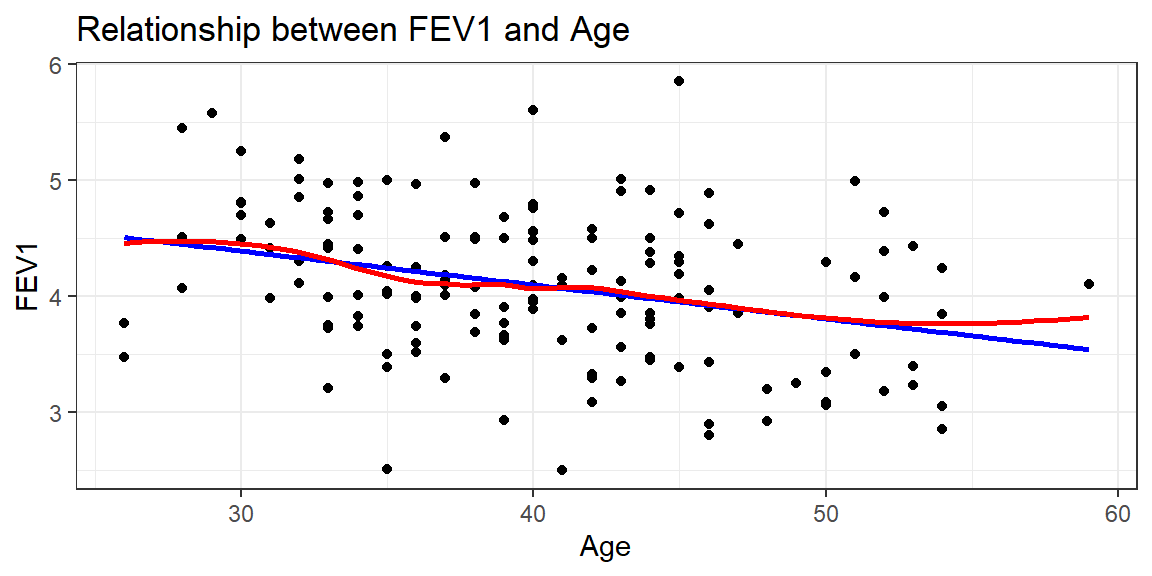
There appears to be a tendency for taller men to have higher FEV1, but FEV1 also decreases with age.


We need to have a robust model that can incorporate information from multiple variables at the same time.

Framework

  • Multiple linear regression (MLR) is our tool to expand our MODEL to better fit the DATA.
  • Describes a linear relationship between a single continuous \(Y\) variable, and several \(X\) variables.
  • Models \(Y\) from \(X_{1}, X_{2}, \ldots , X_{P}\).
  • X’s can be continuous or discrete (categorical)
  • X’s can be transformations of other X’s, e.g., \(log(x), x^{2}\).

Visualization

Now it’s no longer a 2D regression line, but a \(p\) dimensional regression plane.

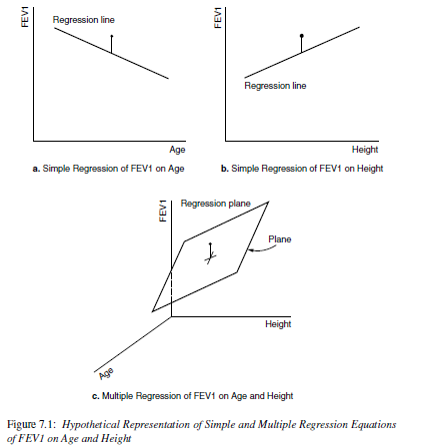
A regression plane in 3 dimensions: \(FEV1 \sim Height + Age\)

Mathematical Model

The mathematical model for multiple linear regression equates the value of the continuous outcome \(y_{i}\) to a linear combination of multiple predictors \(x_{1} \ldots x_{p}\) each with their own slope coefficient \(\beta_{1} \ldots \beta_{p}\).

\[ y_{i} = \beta_{0} + \beta_{1}x_{1i} + \ldots + \beta_{p}x_{pi} + \epsilon_{i}\]

where \(i\) indexes the observations \(i = 1 \ldots n\), and \(j\) indexes the number of parameters \(j=1 \ldots p\).

Assumptions

The assumptions on the residuals \(\epsilon_{i}\) still hold:

  • They have mean zero
  • They are homoscedastic, that is all have the same finite variance: \(Var(\epsilon_{i})=\sigma^{2}<\infty\)
  • Distinct error terms are uncorrelated: (Independent) \(\text{Cov}(\epsilon_{i},\epsilon_{j})=0,\forall i\neq j.\)

Parameter Estimation

Find the values of \(b_j\) that minimize the difference between the value of the dependent variable predicted by the model \(\hat{y}_{i}\) and the true value of the dependent variable \(y_{i}\).

\[ \hat{y_{i}} - y_{i} \quad \mbox{ where } \quad \hat{y}_{i} = \sum_{i=1}^{p}X_{ij}b_{j}\]

AKA: Minimize the sum of the squared residuals:

\[ \sum_{i=1}^{n} (y_{i} - \sum_{i=1}^{p}X_{ij}b_{j})^{2}\]

Fitting the model

Fitting a regression model in R with more than 1 predictor is done by adding each variable to the right hand side of the model notation connected with a +.

Show the code 
mlr.dad.model <- lm(FFEV1 ~ FAGE + FHEIGHT, data=fev)
Show the code 
broom::tidy(mlr.dad.model)
# A tibble: 3 × 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)  -2.76     1.14        -2.43 1.65e- 2
2 FAGE         -0.0266   0.00637     -4.18 4.93e- 5
3 FHEIGHT       0.114    0.0158       7.25 2.25e-11
Show the code 
confint(mlr.dad.model)
                  2.5 %      97.5 %
(Intercept) -5.00919751 -0.51229620
FAGE        -0.03922545 -0.01405323
FHEIGHT      0.08319434  0.14559974
Show the code 
lm(FFEV1 ~ FAGE + FHEIGHT, data=fev) |> 
  tbl_regression(intercept=TRUE) |>
  add_glance_table(include = c(adj.r.squared, nobs))
Characteristic Beta (95% CI)1 p-value
(Intercept) -2.8 (-5.0 to -0.51) 0.016
FAGE -0.03 (-0.04 to -0.01) <0.001
FHEIGHT 0.11 (0.08 to 0.15) <0.001
Adjusted R² 0.325
No. Obs. 150
1 CI = Confidence Interval

The corresponding regression equation now is

\[ \hat{y}_{i} = -2.76 - 0.027(age) + 0.114(height) \]

Interpreting Coefficients

Intercept

The intercept is interpreted as the predicted outcome when all covariates are set to 0.

\[ \hat{y}_{i} = -2.76 - 0.027(age) + 0.114(height) \]

A father who is 0 years old, and is 0 inches tall has an expected FEV of -2.76L

This number that does not make any sense whatsoever. This is often the case, and why regression output tables tend to not show the intercept.

Continuous Predictors

Slope

\(b_{j}\) is the estimated change in \(Y\) for a 1 unit increase in \(x_{j}\) while holding the value of all other variables constant. Can also be phrased as “after controlling for other predictors..”

\[ \hat{y}_{i} = -2.76 - 0.027(age) + 0.114(height) \]

  • \(b_{1}:\) A father who is one year older is expected to have a FEV value 0.027 (0.014, 0.039) liters less than another man of the same height (\(p<.0001\)).
  • \(b_{2}:\) Holding age constant, a father is expected to have 0.11 (.08, 0.15)L greater FEV for every inch taller he is compared to another father (\(p<.0001\)).

Binary Predictors

Reference level coding

  • Binary predictors (categorical variables with only 2 levels) get converted to a numeric binary indicator variable which only has the values 0 and 1.
  • Whichever level is assigned to be 0 is called the reference group or level.

“Slope” as a difference in groups

\(b_{j}\) is the effect of being in group (\(x_{j}=1\)) compared to being in the reference (\(x_{j}=0\)) group.

Model with sex as a predictor

Let’s look at how biological sex may impact or change the relationship between FEV and either height or age. The regression model now is:

\[ y_{i} = \beta_{0} + \beta_{1}x_{1i} + \beta_{2}x_{2i} +\beta_{3}x_{3i} + \epsilon_{i}\]

where

  • \(x_{1}\): Age
  • \(x_{2}\): height
  • \(x_{3}\): 0 if Male, 1 if Female

❌ Do not manually change the variable to binary 0/1 numeric!

Base R

Show the code 
lm(FEV1 ~ AGE + HEIGHT + BIOL.SEX , data=fev_long) |> 
  summary()

Call:
lm(formula = FEV1 ~ AGE + HEIGHT + BIOL.SEX, data = fev_long)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.36151 -0.29656 -0.00458  0.30785  1.42583 

Coefficients:
                Estimate Std. Error t value Pr(>|t|)    
(Intercept)    -2.240511   0.751707  -2.981  0.00312 ** 
AGE            -0.023539   0.004068  -5.786 1.83e-08 ***
HEIGHT          0.105089   0.010527   9.983  < 2e-16 ***
BIOL.SEXFemale -0.637746   0.078324  -8.142 1.09e-14 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.4776 on 296 degrees of freedom
Multiple R-squared:  0.6494,    Adjusted R-squared:  0.6459 
F-statistic: 182.8 on 3 and 296 DF,  p-value: < 2.2e-16

tbl_regression

Show the code 
lm(FEV1 ~ AGE + HEIGHT + BIOL.SEX , data=fev_long) |> 
  tbl_regression(intercept=TRUE) |> 
  add_glance_table(include = c(adj.r.squared, nobs))
Characteristic Beta (95% CI)1 p-value
(Intercept) -2.2 (-3.7 to -0.76) 0.003
AGE -0.02 (-0.03 to -0.02) <0.001
HEIGHT 0.11 (0.08 to 0.13) <0.001
BIOL.SEX

    Male —
    Female -0.64 (-0.79 to -0.48) <0.001
Adjusted R² 0.646
No. Obs. 300
1 CI = Confidence Interval

In this model BIOL.SEX is a categorical variable with levels Male and Female, where Male is the first ordered level. The estimate shown is for females compared to males.

Interpretations

The fitted regression equation for the model with gender is

\[ \hat{y} = -2.24 - 0.02*AGE + 0.11*HEIGHT - 0.64*I(BIOL.SEX==`Female`) \]

  • \(b_{0}:\) For a male who is 0 years old and 0 cm tall, their FEV is -2.24L.
  • \(b_{1}:\) Holding sex and height constant, for every additional year older an individual is, their FEV1 decreases by 0.02L.
  • \(b_{2}:\) Holding age and sex constant, for every additional cm taller an individual is, their FEV1 increases by 0.16L.
  • \(b_{3}:\) Controlling for height and age, females have 0.64L lower FEV compared to males.

Still can use template language

The interpretation of categorical variables still falls under the template language of “for every one unit increase in \(X_{p}\), \(Y\) changes by \(b_{p}\)”. So a 1 “unit” change is females (\(X_{3}=1\)) compared to males (\(X_{3}=0\)).

Categorical Predictors

Residental area

Let’s consider the effect of city environment on FEV. For those unfamiliar with the region, these cities represent very different environmental profiles.

Characteristic N = 300
AREA, n (%)
    Burbank 48 (16)
    Lancaster 98 (33)
    Long Beach 38 (13)
    Glendora 116 (39)

I do not do anything to the variable AREA itself aside from add it into the model.

Base R

Show the code 
lm(FEV1 ~ AGE + HEIGHT + BIOL.SEX + AREA , data=fev_long) |>
  summary()

Call:
lm(formula = FEV1 ~ AGE + HEIGHT + BIOL.SEX + AREA, data = fev_long)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.32809 -0.29573  0.00578  0.31588  1.37041 

Coefficients:
                Estimate Std. Error t value Pr(>|t|)    
(Intercept)    -2.250564   0.752414  -2.991  0.00302 ** 
AGE            -0.022801   0.004151  -5.493 8.59e-08 ***
HEIGHT          0.103866   0.010555   9.841  < 2e-16 ***
BIOL.SEXFemale -0.642168   0.078400  -8.191 8.10e-15 ***
AREALancaster   0.031549   0.084980   0.371  0.71072    
AREALong Beach  0.061963   0.104057   0.595  0.55199    
AREAGlendora    0.121589   0.082097   1.481  0.13967    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.4777 on 293 degrees of freedom
Multiple R-squared:  0.6529,    Adjusted R-squared:  0.6458 
F-statistic: 91.86 on 6 and 293 DF,  p-value: < 2.2e-16

tbl_regression

Show the code 
lm(FEV1 ~ AGE + HEIGHT + BIOL.SEX + AREA , data=fev_long) |> 
  tbl_regression(intercept=TRUE) |> 
  add_glance_table(include = c(adj.r.squared, nobs))
Characteristic Beta (95% CI)1 p-value
(Intercept) -2.3 (-3.7 to -0.77) 0.003
AGE -0.02 (-0.03 to -0.01) <0.001
HEIGHT 0.10 (0.08 to 0.12) <0.001
BIOL.SEX

    Male —
    Female -0.64 (-0.80 to -0.49) <0.001
AREA

    Burbank —
    Lancaster 0.03 (-0.14 to 0.20) 0.71
    Long Beach 0.06 (-0.14 to 0.27) 0.55
    Glendora 0.12 (-0.04 to 0.28) 0.14
Adjusted R² 0.646
No. Obs. 300
1 CI = Confidence Interval

What’s going on?

  • Binary indicators variables were automatically created where a 1 indicates if a person is from that area.
    AREA         AREALancaster AREALong Beach AREAGlendora
1   "Burbank"    "0"           "0"            "0"         
185 "Glendora"   "0"           "0"            "1"         
49  "Lancaster"  "1"           "0"            "0"         
150 "Long Beach" "0"           "1"            "0"
  • Someone from Burbank has 0’s for all of the three indicator variables
  • Someone from Lancaster only has a 1 in the AREALancaster variable and 0 otherwise.
  • Etc for each other area. This is called factor coding (aka “dummy coding”, reference coding, or one-hot encoding)

Process for reference coding.

  • For a nominal variable \(X\), with \(K\) categories, define \(K\) indicator variables.
  • Choose a referent category and leave it out
  • Use remaining \(K-1\) in the regression.
  • Often, the largest category is chosen as the reference category.

Do not have to manually do this

This is automatically done by the software for you in most programs

Mathematical model

\[ Y = \beta_{0} + \beta_{1}*x_{age} + \beta_{2}x_{ht} + \beta_{3}x_{sex} + \beta_{4}x_{4} + \beta_{5}x_{5} + \beta_{6}x_{6} \]

where

  • \(x_{4}=1\) when AREA='Lancaster', and 0 otherwise
  • \(x_{5}=1\) when AREA='Long Beach', and 0 otherwise
  • \(x_{6}=1\) when AREA='Glendora', and 0 otherwise

The coefficients for the other levels of the categorical variable are interpreted as the effect of that variable on the outcome in compared to the reference level.

Interpreting coefficients

Show the code 
lm(FEV1 ~ AGE + HEIGHT + BIOL.SEX + AREA , data=fev_long) |> 
  tbl_regression(intercept=TRUE) |> 
  add_glance_table(include = c(adj.r.squared, nobs))
Characteristic Beta (95% CI)1 p-value
(Intercept) -2.3 (-3.7 to -0.77) 0.003
AGE -0.02 (-0.03 to -0.01) <0.001
HEIGHT 0.10 (0.08 to 0.12) <0.001
BIOL.SEX

    Male —
    Female -0.64 (-0.80 to -0.49) <0.001
AREA

    Burbank —
    Lancaster 0.03 (-0.14 to 0.20) 0.71
    Long Beach 0.06 (-0.14 to 0.27) 0.55
    Glendora 0.12 (-0.04 to 0.28) 0.14
Adjusted R² 0.646
No. Obs. 300
1 CI = Confidence Interval
  • \(b_{0}\): For a male who lives in Burbank, is 0 years old and 0in tall has an expected FEV1 of -2.3L.
  • \(b_{4}\) Controlling for age, height and biological sex, a person who lives in Lancaster has .03 (-.14, .20) higher lung function than a person living in Burbank.
  • \(b_{5}\) Controlling for age, height and biological sex, a person who lives in Long Beach has .06 (-.14, .27) higher lung function than a person who lives in Burbank.
  • \(b_{6}\) Holding other variables constant, a person who lives in Glendora has .12 (-.04, .28) higher lung function than a person who lives in Burbank.

None of these differences are significant, so we can conclude that after controlling for age, height and biological sex, residential area does not have an effect on the persons lung function. This can also be noticed by the lack of increase in the \(R^{2}\) value compared to the simpler model

🔗 https://math615.netlify.app / Multiple Linear Regression